「Halide: A Language and Compiler for Optimizing Parallelism, Locality, and Recomputation in Image Processing Pipelines」の邦訳と感想(その1)
最近、趣味の実装にばかり時間を割いていたため、また前の投稿から少し空いてしまったが、
今書き溜めていている分を少しずつ公開していくことにしようと思う。
今回から2回にかけて画像処理用DSLのHalideの論文を訳を公開していこうと思う。元から素晴らしい技術であったが、近年のDeepLearningブームで再度脚光を浴びつつあるように感じる。
お恥ずかしながら、実は主もその名前は知ってはいたが、内容を読んだのはDLブームの後のことである。(^q^)
最近ではTVM-NNVMフローなんかでも主要な技術として応用されている。
本家: http://halide-lang.org/
より詳しい長編版:
https://people.csail.mit.edu/jrk/halide12/halide12.pdf
「Halide: A Language and Compiler for Optimizing Parallelism, Locality, and Recomputation in Image Processing Pipelines」の邦訳と感想(その1)
# Abstract
画像処理パイプラインはステンシル計算とストリームプログラムの挑戦の組み合わせである。それらはグローバルまたはデータ依存のアクセスパターンを含むステージと複雑なリダクション処理、異なるステンシルステージの巨大なグラフから構成される。その複雑な構成から、ナイーブな実装と最適化された実装の性能の違いが桁違いになることも珍しくない。効率的な実装は並列性と局所性の双方の最適化を必要とする。しかし、ステンシルの性質から、並列性と局所性および共有データの余分な再計算の導入は基本的に対立している。
我々は、ステンシルパイプラインへの基本的空間と画像処理パイプラインの各ステージ内における基本的空間のトレードオフのシステマティックなモデルと、画像処理パイプラインの各段階でその具体的点な点を記述する”スケジュール”表現、およびHalideアルゴリズムとスケジュールによる高性能な実装を合成するHalide画像処理言語の最適化コンパイラを提供する。このコンパイラをスケジュール空間上の確率的検索と組み合わせることにより、SIMDを用いたマルチコアやCPU+GPUの混成環境を含む異なるハードウェアアーキテクチャの上で、構成可能なプログラムはSOTAな性能を広範囲の実画像処理のパイプラインに対して達成することができるようになる。過去の自動コンパイラの範囲を超えた画像処理アプリケーションのため、我々は数時間でかけてしまう単純なHalideプログラムが、数週間または数ヶ月にわたる専門家の手作業によって最適化されたCや組み込み関数、CUDA実装よりも、最大で5倍の高速な性能になることを実証する。
Introduction
画像処理パイプラインは様々なところにあり、数え切れないカメラや画像センサーによって集められた仮想情報の運河をキャプチャ、分析、採掘、描画するために必要不可欠である。生の画像処理アプリケーション、物体の検出と認識、マイクロソフトのKinect、InstagramとPhotoshop、医療のイメージングと神経スキャニングなどの全ては、急激な解像度の上昇やイメージセンサのフレームレート、アルゴリズムの複雑性の増加に対処するために極めて高い性能を要求する。同時に、カメラやモバイルデバイスの縮小化は、バッテリーパワーの上で数分以上動作し続けるために、極めて高い効率性を必要とする。電力消費の多いラジオやビデオコーデックがカスタムハードウェアの上で変化の遅い標準として実装されてきた一方で、画像処理ハードウェアは急速に進化および多様化して、高性能なソフトウェア実装を要求している。
画像処理パイプラインのステンシル計算とストリームプログラムにおける挑戦の組み合わせである。それらは沢山の異なる命令の巨大なグラフからなっており、その殆どはステンシル計算である。これらのパイプラインは巨大であると同時に深い。それぞれのステージは計算する必要のある多くのピクセルにまたがるデータ並列性を持ち、全体のパイプラインは個別では低い算術強度を持つ異なる演算の長いシーケンスからなる。例えば、1つの最近のアルゴリズムの実装であるローカルラプラシアンフィルタは、大量のことなあるステンシルと巨大なデータ依存の再サンプリングを含む、99の異なるステージのグラフである。
このような構成の結果として、そのパイプラインのナイーブな実装と高度に最適化されたものとの性能の違いは一桁以上になることも珍しくない。現在のツールを用いても、殆どの場合でピーク性能に近づくための唯一の方法は手作業による低レベルのCやCUDA、組み込み関数、アセンブリなどを並列化、ベクトル化、タイル化、大域的コード融合化である。単純なパイプラインは数百行の難解で交互的なコードになり、Adobeのカメラローエンジンのような複雑なパイプラインは数十万行にも登る。それらのチューニングは専門的プログラマの多大な労力を必要とするが、その最終的な結果は、苦労して得られた性能の殆どを犠牲にすることなくしては、異なるアーキテクチャに移植することも、他のアルゴリズムとの組み合わせることもできない。最適化されたサブルーチンのライブラリもまたこの問題を解決できない。なぜなら、多くの重要な最適化はプロデューサ-コンシューマのローカリティをステージ間で融合しているためである。
我々は抽象度のレベルを上げることとアルゴリズムの定義を実行ストラテジから分離することにより、可搬性と再編成性を向上の問題に対処する。また同時に、結果として得られる並列マシンや複雑なメモリ階層に対するパイプラインの最適なマッピングの検索を自動化する。効果的な抽象化と最適化の自動化は、より単純なプログラムが広範囲のアーキテクチャに及んで動作しながらも、エキスパートが手でおこなった実装より高い性能を達成することを可能にする。
1.1 Image Processing Pipelines
ステンシルは科学的アプリケーションの反復によるステンシル計算の形体でよく研究されている。それらは1つまたは少数の小さなステンシルが多くの反復を通じて同じグリッドに適用される。対象的に、我々は画像処理とコンピュータグラフィックスにおける異なるアプリケーションに興味がある。ステンシルは一般的だが、それらはしばしば全く異なる姿をしている。ステンシルパイプラインは異なるステンシル計算のグラフである。同じステンシルの繰り返しが発生するが、これはルールではなく例外である。ほとんどのステージでは次のステージにデータを渡す前に一度だけステンシルを適用し、別のステンシルでは異なるデータ並列計算を実行する。
グラフ構造プログラムはストリーミング言語の背景で研究されてきた。静的通信分析を使用すると、ストリームコンパイラは、カーネル間の計算と通信をインタリーブすることによって、データの並列性とプロデューサ-コンシューマのローカリティを同時に最適化できる。しかしながら、殆どのストリーム計算の研究は1次元のストリームに着目してきており、スライディングウィンドウの通信では一次元のステンシルのパターンが許されている。画像処理パイプラインは2次元または3次元のストリームとステンシル上のだと考えることができる。また、画像処理に必要とされる計算モデルはステンシル単体より一般的である。殆どのステージが前のステージの結果を用いたポイントまたはステンシル演算であるが、幾つかのステージはデータをそれに依存した任意のアドレスからギャザーしたり、ヒストグラムのような演算を計算するために任意のアドレスにスキャターしたりする。
ループフュージョンは各ポイントにおける複数の連続した演算を1つの合成された演算に融合することで、プロデューサ-コンシューマローカリティを最大化し算術強度を改善し、データがパイプラインを通して流れるように中間データを高速なローカルメモリに保持する。シンプルなmap演算のパイプラインはこの伝統的なループフュージョンで最適化できる。しかし、伝統的なループフュージョンはコンシューマステージ内の近接したポイントがプロデューサステージの領域に依存している際、ステンシル演算を適用することができない。代わりに、ステンシルはプロデューサ-コンシューマローカリティと同期化、冗長計算における複雑なトレードオフを必要とする。なぜなら、このトレードオフは各ステージ での割り当て、実行、計算、通信の順番がインタリーブする事により生み出されるためである。我々はこれをパイプラインの”スケジュール”と呼ぶ。これらのトレードオフは科学的アプリケーション内の個々の反復されたステンシル演算の中に存在し、選択した空間の複雑度には、過去の研究から導入された多くの異なるタイリングとスケジューリング戦略が反映されている。画像処理パイプライン内では、このトレードオフはグラフ内のステージ(時には十から百に及ぶ)間の各プロデューサ-コンシューマ関係によって生み出されるべきであり、理想的にスケジュールは全てのステージ間のグローバルな相互作用に依存する。これは、しばしば多くの異なる戦略の組成を必要とする。
1.2 Contributions
Halideはモダンな計算フォトグラフとビジョンアプリケーションにみられる複雑な画像処理パイプラインのためのオープンソースのDSLである。本稿ではこの言語への最適化コンパイラを提案する。我々は以下の導入する。
- ステンシルパイプラインにおけるローカリティと並列性、冗長な再計算 のトレードオフ の体系化されたモデル
- その選択肢の空間を結ぶスケージューリング表現
- その空間内のいかなる点も合成するために、Halideプログラムとスケジュールラ記述を組み合わせた表現に基づいたDSLコンパイラ。これはどのようにプログラムを実行するかを、その何を計算すべきかの定義からだけでなく、コンパイラのブラックボックスの外から引き出された全ての方法から分離するデザインを利用する。
- 単純なインターバル分析に基づいたデータ並列パイプラインのためのループ合成機。これは多面体モデルより簡単で表現力が低いが、これが分析できる表現のクラスではより一般的である。
- 高性能なベクターコードを提供するコードジェネレータ。これ多面体モデルよりも十分に単純な過程を用いる。
- 確率的検索を利用した複雑な画像処理パイプラインのための、高性能スケジュールを推論することができるオートチューナ。このスケージュールは専門家によって書かれた手作業で最適化されたプログラムよりも最大で5倍高速である。
我々のスケジューリング表現は、局所性、並列性、冗長な作業の回避におけるトレードオフの範囲を組み合わせてモデル化する。これは、殆どの以前のステンシルの最適化と同時にそれらの階層的な組み合わせを自然と表現することができる。以前のステンシルコード生成と違い、ただ単一のステンシルスケジューリング戦略を述べることはせず、ステンシルと他の画像処理計算グラフの中にある、全てのプロデューサ-コンシューマエッジを別々に扱う。 この分離表現は、スケジュールとその下にあるアルゴリズムを分離し、コンパイラの裏表のデザインと組み合わせられることで、このコンパイラが自動的に最適なスケジュールを探索することを許す。数百の内部依存の次元により、可能なスケジュールの空間は膨大にある。これは多面体最適化または既存の既存のステンシルコンパイラとオートチューナーに採用されている素晴らしいパラメータ探索には大きすぎる。しかしながら、我々は確率的探索を用いることで、高性能なスケジュールを発見することが可能であることを示す。 与えられたスケジュールに、我々のコンパイラは自動的に高性能な並列ベクタコードを生成する。例えば、SSE/AVXやNEONを用いたx86やARM CPUのコード、ハイブリットGPU実行のためのホスト管理コードと折り合わせられたCUDAカーネルのグラフなどである。これは内部割り当てと、シンプルだが汎用性のあるインターバル分析を用いた完全なループネストを自動的に推論する。SIMD実行へのデータ並列次元の直接的なマッピングすることと、ストライドされたアクセスパターンの注意深い処理を含むことは、任意の汎用目的のループ自動ベクトル化を必要とせずに、高性能ベクタコードの生成を可能にする。 最終的な結果は、広範囲の実画像処理パイプラインに対して、SIMDやCPUとGPU実行の混成環境を含む異なるハードウェアにおいて、簡素で組み合わせ可能なプログラムがSOTAな性能を達成した。過去の自動コンパイラを超えた画像処理アプリケーションのため、我々は数時間で書かれた単純なHalideプログラムにより、専門家により数週間から数ヶ月かけて書かれたハンドチューンのC、組み込み関数、CUDA実装より最大で5倍高速な性能が得られたことを実証する。
2. The Halide DSL
我々はシンプルな関数のスタイルで画像処理パイプラインを記述するために、Halide DSLを用いる。単純なC++実装のローカルラプラシアンフィルタであっても数十のループネストと数百行のコードで記述される。これは伝統的なループ最適化システムを用いて、大域的に最適化されているため実用的ではない。このHalide版は、元の実装を62行に短縮し、その本質的なデータフローと計算を99のステージパイプライン内で記述している。また、どのようにそのプログラムが合成されるかの選択も個別に記述されている。
Halideでは、命令形言語でミュータブルな配列となるであろう値は、代わりに座標から値への関数となる。これは画像を無限整数空間に於いて定義される純粋関数として表現する。ある点でのその関数の値は、その対応するピクセルにおける色として表現される。また、パイプラインは関数のチェインルールで指定される。関数は引数の単純式でも、有界のリダクションでも良い。その関数を副作用無しで定義する式は、以下で述べる項目を含む単純関数型言語によく似ている。
- 算術論理演算
- 外部画像からのロード
- if-else式
- 名前付き変数への参照(これらはおそらく関数の引数または、関数型のlet構築子によって定義された式)
- 外部CのABI関数を含む、他の関数の呼び出し
例えば、分離可能な3 x 3非正規化ボックスフィルタは、以下のように$x, y$を用いた2つの関数の連鎖で表現できる。
UniformImage in(UInt(8), 2) Var x, y Func blurx(x,y) = in(x-1,y) + in(x,y) + in(x+1,y) Func out(x,y) = blurx(x,y-1) + blurx(x,y) + blurx(x,y+1)
この表現はほとんどの関数型言語よりシンプルである。これは高階関数や動的再帰、リストのような追加のデータ構造も含んでいない。
関数は整数の座標からスカラーの結果へ単純にマップされている。高階関数のようなもっと高度に制約付けされたものはシンタックスシュガとして追加されるが、基本的な表現を変更することはない。
この表現は広範囲の画像処理アルゴリズムを記述するために重要であり、この制約はコンパイル時におけるアルゴリズムの柔軟な分析や変換を可能にする。クリティカルには、この表現は自然に各関数の領域内でデータ並列である。また、関数が無限領域において定義されるため、追加の値の任意のガードバンドは必要に応じて計算され、境界条件は安全かつ効率的に扱われる。アライメントのような性能上の問題や安全性のために、ガードバンドは画像処理コードにおいてよく見られるパターンである。特定の境界条件がアルゴリズムの意味に関係する場合は、その関数が独自の境界条件を定義することができる。
Reduction function
ヒストグラムや汎用コンボリューションのような演算を表現する場合、サメンション、ヒストグラム、スキャンのような、反復や再帰的な計算を表現する方法が必要である。リダクションは2つの部分から定義され
る。
- 初期値関数:
出力領域の各点において値を指定する。 - 再帰的リダクション関数:
依然に計算された値において、出力座標表現により与えられた点上の値を再定義する。
純粋関数と違い、リダクション関数の意味はそれが適用された順序に依存する。プログラマは各次元の最小値と最大値の式で囲まれたリダクション領域を定義することで、その順序を指定する。出力領域における各点の値は、そのリダクション領域を辞書式順序で再帰した後、その点におけるリダクション関数の最終値によって定義される。
このパターンはアルゴリズムの範囲を伝統的なステンシル計算のスコープの外で記述するが、これは副作用を制限する方法として画像処理パイプラインに必須である。例えば、ヒストグラム均一化は複数のリダクションとデータ依存ギャザーの組み合わせである。スキャタリングリダクションでヒストグラムを計算し、再帰的スキャンでそれをCDF(Cumulative Distribution Fuction, 累積分布関数)に統合、CDFを用いたポイントワイス演算で入力をリマップする。
UniformImage in(UInt(8), 2); // リダクション領域 RDom r(0..in.width(), 0..in.height()), ri(0..255); Var x, y, i; Func histogram(i) = 0; histogram(in(r.x, r.y))++; // スキャタリングリダクション: ヒストグラムを計算 Func cdf(i) = 0; cdf(ri) = cdf(ri-1) + histogram(ri); // 再帰的スキャン: 累積分布関数の計算 Func out(x, y) = cdf(in(x, y)); // ポイントワイス演算: 出力のx,yにおける累積分布関数値を書き込み
リダクションとスキャンにおけるイテレーションの境界は、プログラマが用いる明示的なリダクション領域(RDom)によって表現される。
3. Scheduling Image processing pipeline
画像処理アルゴリズムのHalide表現は、実行の順番やデータの位置に対する制約を課すことを避けます。値はそれが利用可能になる前に計算される必要があり、アルゴリズムにおける基本的な依存を尊重しつつ、多くの選択肢(以下に示す)を未指定のままにしておく。
- 各関数の各座標が、いつどこで計算されるべきか
- それらはどこに保存されるべきか
- どのくらいの長さ値をキャッシュされるまたは複数のコンシューマを介して計算されるのか。また、それらはいつ独立して再計算されるのか。
これらの選択はそのアルゴリズムの結果が保つ意味を変更することはないが、結果として得られる実装の性能には不可欠である。我々はいつどこで値が計算されるのかを、パイプラインのスケジュールと呼ぶ。
ステンシルアクセスパターンでは、それらの選択がプロデューサ-コンシューマローカリティ、並列性、共有値の冗長な再計算という要素が持つ根本的な対立によって制約される。
3.1 Motivation: Scheduling a Two-Stage Pipeline
単純な2ステージのぼかしアルゴリズムを考える時、これは3x3ボックスフィルタを2つの3x1のパスとして計算する。まず、初めのステージblurxは、3x1ウィンドウを用いた入力の平均化により水平方向のぼかしを行う。
blurx(x, y) = in(x-1, y) + in(x, y) + in(x+1, y)
その後、outは初めのステージの出力値を1x3ウィンドウで平均化することにより、最終的に等方的なぼかしを計算する。
out(x, y) = blurx(x, y-1) + blurx(x, y) + blurx(x, y+1)
出力ステージの観点からパイプラインのスケジューリングについて考える自然な方法は、"どのように入力を計算すべきかである"。ここにはパイプラインのための3つの明らかな選択肢がある。
初めに、outにおける任意の点を評価する前に、blurx内で要求される全ての点を計算及び格納することができるだろう。これが6メガピクセル(3k x 2k)の画像に適用されると、それは以下のループネストと等価になる。
alloc blurx[2048][3072]
for each y in 0..2048:
for each x in 0..3072:
blurx[y][x] = in[y][x-1] + in[y][x] + in[y][x+1]
alloc out[2048][3072]
for each y in 1..2047:
for each x in 0..3072:
out[y][x] = blurx[y-1][x] + blurx[y][x] + blurx[y+1][x]
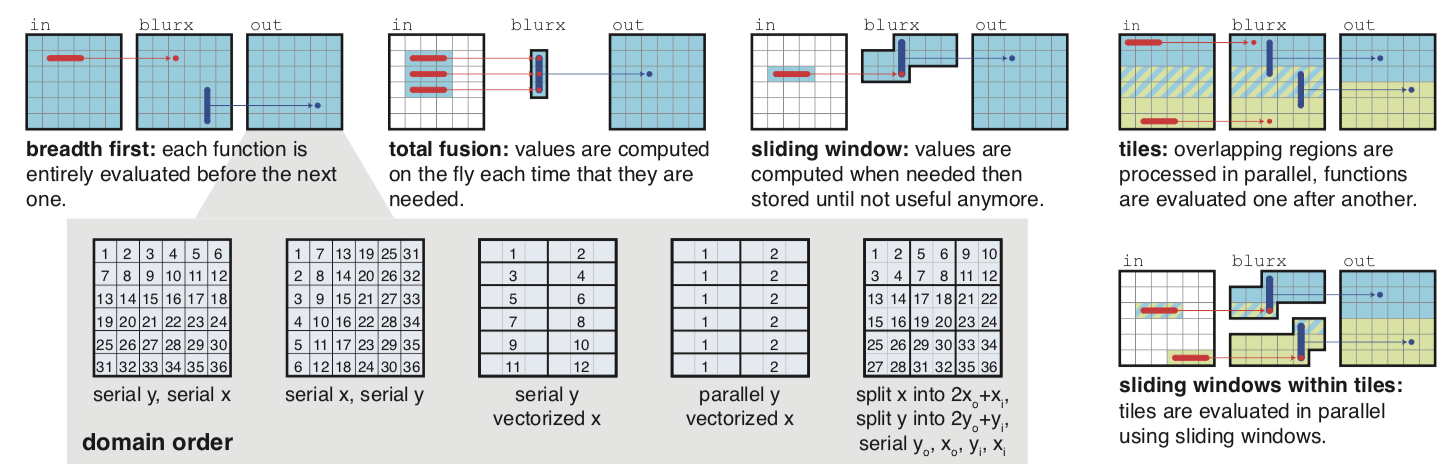
これは手で作成したパイプラインで最も一般的な方法であり、ライブラリルーチンを一緒に合成した結果、次のステージへの全体的な出力を渡す前に、各ステージは幅優先で実行を行う。これらは各ステージにおける必要とされる全てのポイントにおいて、独立した計算および格納ができるため十分な並列性が存在する。しかし、全てのblurxの値はoutで利用される前に計算および格納されなければならないため、いくらかのプロデューサ-コンシューマローカリティがあるとも言える。
他の方法として、outステージは、それを使用するポイントの直前にblurxの各ポイントを計算することができる。これらは、「複数のoutのポイントに利用されるblurxのポイントは再利用されるべきか?または各コンシューマによって独立して再計算されるべきか?」というさらなる選択肢を生む。
2つのステージをインターリーブして中間結果をその利用のために保存する事なしに2つのステージをインターリーブすることは、以下のループネストと等価になる。
alloc out[2046][3072]
for each y in 1..2047:
for each x in 0..3072:
alloc blurx[-1..1]
for each i in -1..1:
blurx[i] = in[y-1+i][x-1] + in[y-1+i][x] + in[y-1+i][x+1]
out[y][x] = blurx[0] + blurx[1] + blurx[2]
各ピクセルは独立して計算することができ、幅優先戦略により同じ量の並列性を提供する。プロデューサとコンシューマの距離は小さく、局所性を最大化する。しかし、blurxの共通値はイテレーションの通して再利用されないため、この戦略は冗長に働く。これは古典的なループヒュージョンをステンシル依存のパターンに適用したものと見なすことができる: 初めのループの本体は次のループに移されるが、その作用はステンシルのサイズにより増幅される。
2つのステージは、blurxの値を利用に際して格納する間にインターリーブさせることができる。
alloc out[2046][3072]
alloc blurx[3][3072]
for each y in -1..2047:
for each x in 0..3072:
blurx[(y+1)%3][x] = in[y+1][x-1] + in[y+1][x] + in[y+1][x+1]
if y < 1: continue
out[y][x] = blurx[(y-1)%3][x]
+ blurx[ y % 3 ][x]
+ blurx[(y+1)%3][x]
これはスライドウィンドウ上で計算をインターリーブし、outはblurxそのステンシル半径(1スキャンライン)だけ追跡する 。これは無駄なく動作する。なぜなら、blurxの各点における計算はたった一度しか行わず、かつblurxにより生成される値と、それがoutによって消費される間の最大距離は、イメージ全体ではなくステンシルの高さ(3スキャンライン)に比例するためである。しかしこれを達成するために、ループイテレーション間の依存が発生する。例えば、outのイテレーションはblurxにおける最後3つの外側イテレーションに依存する。これは、これらのループが順番に連続して評価される場合でのみ上手くいく。各値をただ一度だけ生成しつつステージのインターリーブを行うことは、計算の順番における厳しいな同期を必要とし、並列性を犠牲にする。
これらの各戦略は有名な潜在的欠点を持っている。それはローカリティの損失、冗長な動作、並列性の制限である(図2,3)。実用的には与えられたパイプラインに対する正しい選択は、常にこれらの手法の間の何処かにある。我々の2ステージからなる例では、blurxの計算をインターリーブし、タイルレベルでoutを行うことで良いバランスが得られる。
alloc out[2046][3072]
for each ty in 0..2048/32:
for each tx in 0..3072/32:
alloc blurx[-1..33][32]
for y in -1..33:
for x in 0..32:
blurx[y][x] = in[ty*32+y][tx*32+x-1]
+ in[ty*32+y][tx*32+x]
+ in[ty*32+y][tx*32+x+1]
for y in 0..32:
for x in 0..32:
our[ty*32+y][tx*32+x] = blurx[y-1][x]
+ blurx[y ][x]
+ blurx[y+1][x]
これはタイル内と全タイル間の両方において並列性を損なうことなく、タイル同士の境界における小さな冗長計算と引き換えに、十分に大きいプロデューサ-コンシューマローカリティを得ことができる。余談だが、反復的ステンシル計算の常識において、冗長計算の領域はしばしば“ghost zone”と呼ばれ、このような戦略のことをよく“overlapped tiling”と言う。モダンなx86において、この戦略は同量のマルチスレッドとベクトル並列を用いた幅優先戦略より10倍速くなる。これはプロデューサ-コンシューマローカリティの欠如が、幅優先の手法をバンド幅により制限されたままにするためである。この違いはパイプラインが長くなり、入力と出力間の中間データの割合が増えるほど顕著になる。これはムーアの法則に従って、計算資源がメモリ帯域より指数的に速く増えていくこと限り増加していくだろう。
我々がこのアーキテクチャの上で発見した最も高速な戦略は、画像を別々に扱われる独立した幾つかのスキャンラインのストリップ(細い区間)に分割し、スキャンライン上でスライディングウィンドを用いることで、2つのステージの計算をインターリーブさせることである。
alloc out[2046][3072]
for each ty in 0..2048/8:
alloc blurx[-1..1][3072]
for y in -2..8:
for x in 0..3072:
blurx[(y+1)%3][x] = in[ty*8+y+1][x-1]
+ in[ty*8+y+1][x]
+ in[ty*8+y+1][x+1]
if y < 0: continue
for x in 0..3072:
out[ty*8+y][x] = blurx[(y-1)%3][x]
+ blurx[ y % 3 ][x]
+ blurx[(y+1)%3][x]
論文のオリジナルコードはx次元でin[ty*8+y+1][tx*32+x-1]となっているが、ここではtx次元は存在しない(というかxがtx次元の境界??)ため間違っているかも??
(゜.゜)
元のスライディングウィンドとは相対的に、独立して処理されたblurxストリップの上端と下端に重複した2つのスキャンラインを犠牲にして、各スキャンライン内の細粒度の並列性とスキャンラインストリップ間の粗粒度の並列性を再利用する。結果は1つのベンチマークマシンにおいてはタイル戦略より10%早かったが、他のベンチマークでは10%遅かった。これらと他の多くの戦略における最適な選択は、そのターゲットアーキテクチャにより変わってくる。大規模なパイプラインでは各ステージの意思決定にグローバルな影響があるため、理想的な選択は個々のステージだけではなく、ステージの構成によって異なる。実画像処理パイプラインはしばしば数十から数百のステージがあり、選択空間の決定は膨大になる。
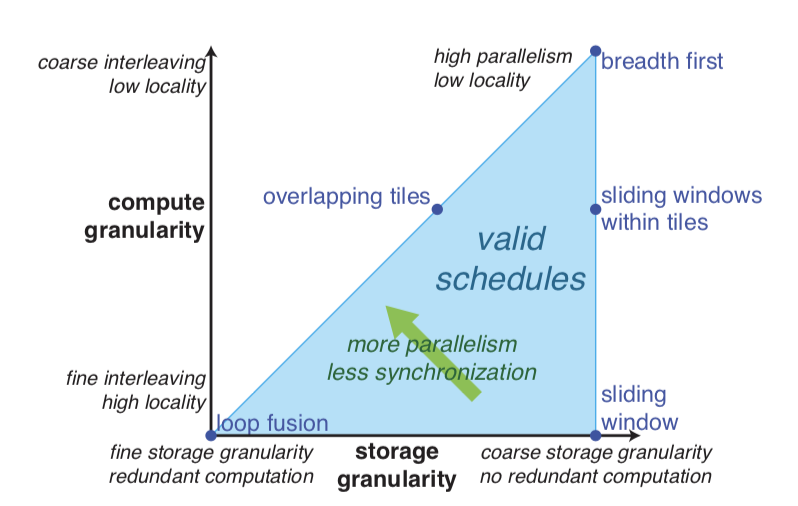
図2
ストレージの粒度($x$-axis)と計算の粒度($y$-axis)による、選択肢スケージューリングの空間を可視化するための自然な方法。
幅優先実行は粗粒度計算は粗粒度のストレージに変換される。全融合すると細粒度の計算は細粒度のストレージ(小さな一時バッファ)に実行する。スライディングウィンドウ戦略は全体の中間ステージにおいて十分な空間を割り当てるが、それをできるだけ遅く細粒度に計算する。これらの手段はそれぞれの潜在的欠点を持っている。幅優先実行はローカリティが、完全融合は冗長な計算を、スライディングウィンドを用いることは、冗長計算を避けるためのループイテレーションにおける依存性により制約される。一番良い方法は往々にしてそれらを組み合わせ、その空間の中間地点に配置することである。
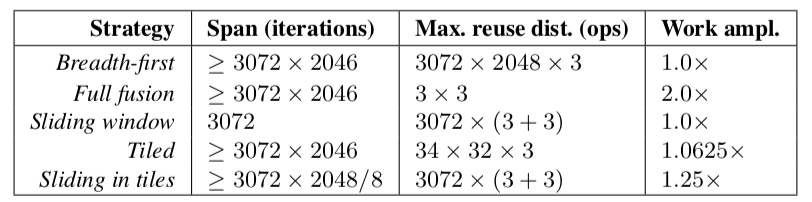
図3
図2における選択空間内の異なる点は、それぞれローカリティと冗長な再計算、並列性間におけるトレードオフを生み出す。この図は、我々の2ステージからなるぼかしパイプラインの効果を定量化している。
- Span: 意味のある処理において、どれくらいの数のスレッドまたはSIMDレーンをビジーに保つことができるかをカウントすることで、利用可能な並列性度を測定
- Max reuse distance: 値の計算とそれを再度読み取る間に発生する操作の最大数を数えることによってローカリティを測定
- Work amplification: 行った算術演算の数を幅優先のケースと比較することにより、冗長な計算を測定
最初の3つの戦略のそれぞれは選択空間の極点を表しているが、1つだけでは貧弱である。最も高速なスケジューリングは、最後の2行をタイリングするような混合戦略である。
3.2 A Model for the Scheduling Choice Space
我々はステンシルパイプラインにおけるスケジューリングの重要な選択子空間のためのモデルを導入する。これは、その入力を計算するためのどの粒度を選択するのか、それぞれを再利用の際にどれほどの粒度で格納を行うのか、これらの粒度の間でどの順番でその領域を通過させるべきかをという各ステージの選択に基づいている(図4)。
The Domain Order
我々のモデルはまず、各関数の定義域で必要な領域が走査されるべき順番を定義する。我々はこれをドメインオーダと呼び、伝統的なループ変形の概念のセットを用いる。
- 各次元を単一または並行に走査することができる
- 定数サイズの次元はアンロール化またはベクトル化できる
- 次元は並び替えできる(行優先または列優先など)
- 最終的に次元はファクタよって分離され、2つの新しい次元を生成する。外側の次元は前の範囲をファクタで割ったものであり、内側の次元はファクタ内でイテレートされる。分離後、元のインデックスへの参照は$outer \times factor + inner$となる。
再帰的に分割を行うと更に選択肢は増えていき、他の変換と組み合わせた時にタイリングのような多くの共通パターンを可能にする。ベクトル化とアンロール化は、初めに次元をベクトル幅とアンローリングファクタにより分離することでモデル化される。その後、新しい内側の次元をvectorizedまたはunrolledとしてスケジューリングする。なぜなら、Halideの関数モデルは構造によりデータ並列となり、その次元は任意の順番でインターリーブされ、どの次元も単一または並列、ベクトル化されてスケージューリングされる可能性があるためである。
リダクション関数に関しては、リダクションの更新が結合的であるならば、そのリダクション領域の次元は並び替えまたは並列化によりスケジューリングされるだろう。依存のない可変な次元は、純粋関数のように任意の順番でスケジュールされるはずである。
我々のモデルは軸にそって区切られた範囲のみを考慮する。画像処理または他の多くのアプリケーションに対する実用的単純化のため、一般化されたポリトープ(超多面体)は含まない。しかし、これは領域を単純な区間解析により定義または分析することを可能にする。我々のモデルスケジューリングは、後のコンパイラ(各関数とループの評価およびストレージの境界を特定するための推論を行う)に基づいているため、境界解析がHalide言語内のあらゆる表現や構造の分析できることが不可欠である。区間解析は多面体解析のようなモダンな手法より単純であるが、そのデザインに欠かすことができない表現の広範囲 を効率的に解析することができる。
図4
単純なパイプラインがスケジューリング選択肢の膨大な空間を持つように見えたとしても、それぞれの表現は 並列性、ローカリティ、冗長な再計算の間で独自のトレードオフを持っている。各ステージに対する選択肢は2つである。より簡単は選択肢はドメインオーダである。これはスレッド並列、ベクトル化、走査順序(行優先または列優先)から表現される。次元は内側部と外側部に分離することができる。これは選択空間の範囲を再帰的に拡大するが、タイリング戦略を表現できる。各ステージが答えなければならないより複雑な質問は、いつその入力が計算されなければならないかである。選択肢にはすべての依存関係を事前に計算する(幅優先)か、可能な限り遅く値を計算してから、それらを即座に廃棄する(全融合)または、可能な限り遅く値の計算を行うが、前の計算を再利用する(スライディングウィンド)がある。この2つの選択カテゴリは相互に関連している。例えば、最速のスケジュールはしばしば領域を並列に計算されるタイルへと分離し、各タイル内で幅優先またはスライディングウィンドにより計算する。
The Call Schedule
各関数の領域における評価の順番に加えて、そのスケジュールはある関数が依存する各関数におけるストレージおよびその計算内容から、その関数の計算をインターリーブする粒度も同時に指定する。これらの選択をcall scheduleと呼ぶ。我々はあるHalideパイプラインにおけるコールグラフ全体に含まれる各関数に対して唯一のコールスケジュールを指定する。各関数のコールスケジュールは、その関数を格納及び計算している呼び出し側関数のループネストに含まれる各点として定義される(図4の上部)。例えば、前の章の3つの手法をこの軸に沿って見ていくと以下のようになる。
-
幅優先スケジュール
最も粗粒度でblurxの格納と計算を行う。
この粒度のことを、他の全てのループの外側という意味でrootlevel(ルートレベル)と呼ぶ。 -
融合スケジュール
outの最も内側のループ(x)の内で、最も細粒度でblurxの格納と計算を行う。
この粒度において、値は同じイテレーションの中で生産及び消費されるが、各イテレーションで独立に再割当て、再計算しなければならない。 -
スライディングウィンドスケジュール
最も細粒度に計算を行い、ルート粒度(最も粗粒度)で格納を行う。
このインターリーブを用いると、blurxの値はそれが初めて使用されるのと同じイテレーションで計算されるが、イテレーションを通して持続する。このスケジューリングは次に来るループ内で共有の値を再利用するために活用されるが、格納と計算のレベルはループ間で厳密に順序付けされなければならない。従って、後の消費者に共有する値を計算するために、各点の初めにユニークな単一のイテレーションが存在する。
同時にコールスケジュールとドメインオーダは、長方形グリッド上のステンシルパイプラインの演算を定義する。これらの選択を組み合わせることは、熟練者による手作業で最適化された画像処理パイプラインに用いれている共通のパターンの大多数を含むスケジュールを、無限の範囲で定義することができる。
ドメインの順序により定義されたループの変形は、コールスケジュールにより選択された内部ステージのインターリービング粒度と相互に作用する。なぜならこのコールスケジュールは、それが格納または計算すべきループレベルを指定することで定義されるためである。関数呼び出し位置は、その直接の呼び出し関数の最も内側の次元からそれ自体の計算をスケジュールする周囲の次元まで、そのコンシューマへの連鎖を通して任意のループ内で計算または格納されるだろう。
次元の分離することで、そのコールスケジューラがその呼出関数が持つ本来の次元よりも細かい粒度で指定できるようになる。例えば、単体のスキャンラインの代わりにブロック化されたスキャンラインを用いてインターリーブする若しくは、個々のピクセルの代わりにピクセルのタイルを用いる方法がある。全ての計算された値はその結果が格納可能な論理的な場所が必要であり、ストレージの粒度は計算の粒度と等しいまたは粗くなければならない。
Schedule Example
再度、3章で最適化された例を見てみよう。タイリングスケジュールは以下のようにモデル化することができる。
-
outのドメインオーダはsplit(y,32)->ty,y; split(x,32)->tx,x; order(ty,tx,y,x)
これは図4の右端に示されている最も単純なタイルのドメインオーダである。すべての次元は並列に計算されうる。また、xは性能のためにベクトル化される。 -
例における
blurxのコールスケジュールはout内にあるtxの格納と計算の双方のセットである。 -
tx下でblurxのドメインはorder(y,x)にスケジュールされ、xは性能のためにベクトル化される。
並列にタイル化されたスライディングウィンドスケジュールは、`blurx`コールスケジュールを「`out`の`ty`で格納しつつ、より細粒度の`y`次元で計算」とすることでモデル化される。
-
outのドメインオーダはsplit(y,8)->ty,y; order(ty,y,x)である。tyはおそらく並列化され、xは性能のためベクトル化される。yはその際利用のために連続でなければならない。 -
y次元以下にあるblurxのドメインは次元xのみを含み、これはベクトル化される。
コメント
コメントを投稿